هر مثلثی متساوی الساقین است!!
مثلثهای متساوی الساقین ، به آن دسته از مثلثهایی که دو ضلع برابر دارند گفته میشود.
ما ادعا میکنیم که
هر مثلثی متساوی الساقین است!
و البته این ادعا را ثابت میکنیم!
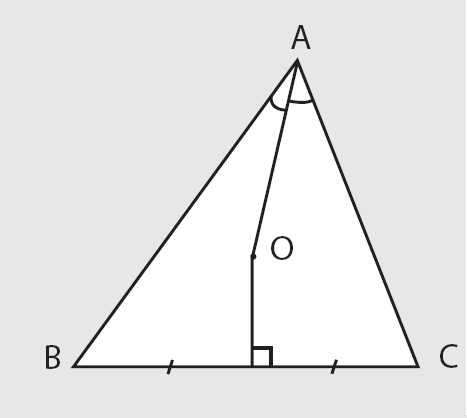
مثلث ABC را در نظر بگیرید. نیمساز زاویهی A و هم چنین عمود منصف ضلع BC را رسم میکنیم. این دو هم را در نقطهای مثل O قطع میکنند.
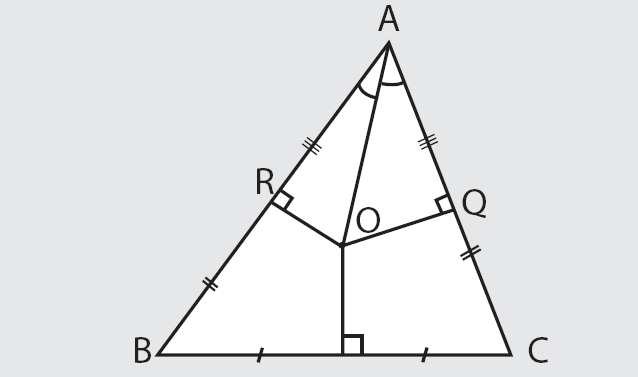
برای اقامهی برهان لازم است که از نقطه O به اضلاع AC و AB عمود رسم کنیم. یعنی چیزی مطابق شکل زیر.

ادعای اول) AR=AQ
اثبات : مثلثهای AOQ و AOR را در نظر بگیرید. ( شکل زیر را ببینید )
در این مثلثها وتر ها برابر هستند یعنی AO=AO و AO وتر هر دو مثلث است.
از طرفی راویهی OAQ و زاویهی OAR برابر هستند چرا که OA نیمساز است.
پس بنابر حالت وتر و یک زاویه ، این دو مثلث قائم الزاویه ( یعنی مثلثهای AOQ و AOR ) هم نهشت هستند که نتیجه میشود اینکه AR=AQ
ادعای دوم) BR=QC
اثبات : شکل زیر را در نظر بگیرید.
در این شکل از آنجا که عمود منصف رسم شده است داریم که BO=OC
از طرفی در ادعای اول ثابت شد که OQ=OR
بنابراین میتوان گفت که مثلثهای قائم الزاویهی BRO و OQC به حالت وتر و یک ضلع با همدگیر هم نهشت هستتند.
که این موضوع نتیجه میدهد که BR=QC

بنابراین ثابت کردیم که
AR=AQ و هم چنین QC=RB با جمع کردن طرفین این دو تساوی داریم که
AR+RB=AQ+QC
AB=AC
پس مثلث ABC حتماً متساوی الساقین است!!!!!
صد البته که این اثبات اشکالی دارد! چرا که بدیهی است که هر مثلثی متساوی الساقین نیست ولی ما این را ظاهراً برای هر مثلثی ثابت کردیم!
سعی کنید اشکال را بیابید.
اخذ شده از مجلهی برهان ، متوسطه اول // این مسئله در مجلهی برهان توسط آقای بهزاد اسلامی مسلّم از یک کتاب خارجی ترجمه شده است.
اسم کتاب خارجی : Fallacies in Mathematics , Cambridge , 1963
نویسنده : Maxwell.E.A
سوالات متداول
هر مثلثی که حداقل دو ضلع برابر داشته باشد را متساوی الساقین می گویند. اگر سومی برابر با دو تای دیگر باشد، متساوی الاضلاع خواهد بود. این مثلث از دوره ی باستان مورد علاقه هندسه دان ها و معمار ها بوده. می توان به راحتی نشان داد برابر بودن دو زاویه مجاور قاعده و شرط متساوی الساقین بودن معادل اند، یعنی یکی دیگری را نتیجه می دهد.
با فرض اینکه می دانیم که دو زاویه مجاور قاعده با یکدیگر برابر اند، از نیمساز بودن خط l نتیجه می شود دو مثلث داریم با زوایای متناظراً برابر، همچنین متساوی الساقین بودن یعنی ضلع میان زوایا هم با یکدیگر برابر اند. در نتیجه بنا بر حالت زضز دو مثلث هم نهشت اند. پس نیمساز در وسط قاعده، آن را قطع کرده است. حال شما از اینکه مجموع سه زاویه مثلث متساوی الساقین 180 درجه است، نتیجه بگیرید که این خط ارتفاع هم هست.

اگر در مثلثی حداقل دو ضلع برابر با یکدیگر داشته باشیم آن مثلث را متساوی الساقین گوییم و به جفت اضلاع مساوی هم ساق مثلث می گویند. این مثل نام گذاری خاص برای وتر، وقتی یک زاویه راست داریم است.
در مثلث متساوی الساقین به ضلعی که بین دو ساق قرار دارد قاعده می گویند. به زاویه روبه روی این ضلع هم زاویه رأس می گویند. زاویه رأس و ضلع قاعده ویژگی های جالبی دارند. به عنوان مثال ارتفاع وارد بر قاعده و میانه آن بر هم منطبق اند. این ارتفاع همچنین بر نیمساز زاویه رأس منطبق است. علاوه بر این همه، ارتفاع وارد بر قاعده محور تقارن مثلث هم هست.
باید توجه داشته باشید مثلث متساوی الساقین طبق تعریف حداقل دو ضلع یکسان خواهد داشت، در نتیجه امکانش هست که در صورت برابر بودن ضلع سوم، یک مثلث متساوی الاضلاع داشته باشیم که به طریق اولی، متساوی الساقین هم هست.
12 دیدگاه
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.


فقط در مثلث های متساوی الساقین نیم ساز زاویۀ مذکور با عمود منصف مذکور در داخل مثلث برخورد می کند و در بقیه مثلث ها چنین نیست
نمی توانیم بگوییم bo=oc بنابراین QcمساویBrنیست.
طبق استدلال های بالا BO=OC کاملاً صحیح است.
شرط تساوی دو مثلث برابری دو ضلع و زاویه بین آنهاست اینجا فقط به تساوی وتر (یک ضلع) و یک زاویه اشاره شده
الان اشکالش کجاست
اشکال کار کجاست
در همهی مثلث ها عمود منصف ضلع با نیمساز زاویه روبه رو به ضلع برخورد نمیکنه تا بتوانیم با چنین استدلالی همهی مثلث هارو متساوی الساقین حساب کنیم و در واقع ایراد اثبات در اینه که محل برخورد عمود منصف یک ضلع و نیمساز زاویه روبه رو به آن در همه ی مثلث ها ، درون مثلث فرض شده است
بسیار اثبات جالبی بود . مشکلش هم اینجاست که عمود منصف یک ضلع و نیم ساز زاویه روبه روش در یک مثلث داخل مثلث یکدیگر رو قطع نمیکنند . برای اثبات کافیه از برهان خلف استفاده کنیم و فرض رو بر این بذاریم که AB و AC برابر نیستند و نیمساز و عمودمنصف یکدیگر رو داخل مثلث قطع میکنند . نتیجه خواهیم گرفت که AB برابر AC است که با فرض مسئله تناقض دارد .
اگر نقطه تلاقی بیرون مثلث بیافتد هم همین استدلال ها وجود دارد و باز اثبات میشود اضلاع برابرند!!
🙂
نکته دیگری که باید به آن توجه کرد این است که باز هم با وجود اینکه محل تلاقی بیرون مثلث میافتد، ممکن است باز هم چنین اثباتی داشته باشیم که باز هم به یک نکته توجه نکردهایم.
در دیدگاه خودم پیشتر اثبات کردم که محل تلاقی روی دایرهی محیطی مثلث است. (به نامگذاریها در دیدگاه من توجه کنید)
چهارضلعی ABXC محاطی
پس BXC=180-BAC
از طرفی پای عمود وارد بر AB از X را Y و پای عمو وارد بر AC از X را Z بگذارید.
در چهارضلعی AYXZ:
دو زاویه ۹۰ داریم پس جمع دو زاویه دیگر
۳۶۰-۹۰-۹۰=۱۸۰ است.
پس
YXZ=180-BAC
که از دو نتیجهای که گرفتیم نتیجه میشود:
BXC=YXZ
که به ما این نتایج را میدهد:
اگر XY درون زاویه BXC باشد، XZ خارج آن است.
اگر XY خارج زاویه BXC باشد، XZ درون آن است.
در مثلثهای متساویالساقین نیز دو زاویه BXC و YXZ منطبق است.
که با این گزارهها که ثابت شد، دیگر نمیتوان چنین اثباتی آورد.
احتمالا در شکل شما هم BY و هم BZ درون زاویه BXC یا هردو بیرون آن هستند که توانستهاید چنین استدلالی کنید.
مشکل این اثبات اینه که هیچگاه عمودمنصف ضلعی از مثلث و نیمساز زاویه روبهروی آن ضلع یکدیگر را در داخل مثلث قطع نمیکنند (به جز مثلث های متساویالساقین که دو خط مذکور بر هم منطبق هستند)
اثبات آن به این صورت است:
دایره محیطی مثلث را میکشیم
عمود منصف ضلع BC دایره را در X قطع میکند.
بنابه قضیه عمودمنصف، BX=CX.
در یک دایره وترهای برابر کمانهای برابر دارند.
پس کمان BX = کمان CX
زاویه BAX = نصف کمان BX
زاویه CAX = نصف کمان CX
پس: BAX=CAX
که یعنی AX همان نیمساز زاویهی BAC است.
که اثبات شد که عمودمنصف ضلعی از مثلث و نیمساز زاویه روبهروی آن ضلع یکدیگر را روی دایرهی محیطی مثلث قطع میکنند که واضح است که درون مثلث نیست.