فرمول استرلینگ
در این نوشته به فرمول استرلینگ میپردازیم. فرمول استرلینگ یک رابطه برای محسابهی تقریبی فاکتوریل اعداد بزرگ است.
فاکتوریل یک عدد طبیعی مثل N که با علامت !N نشان داده میشود، برابر حاصل ضرب تمام عدد طبیعی از یک تا N است. برای مثال :
1x2x3x4= 4! =24
نکته قابل توجه این است که با بالا رفتن N دیگر نمیتوان آن را به سادگی محاسبه کرد و محاسبهی آن قطعاً زمان بر خواهد بود. این در حالیست که برای
محاسبهی حاصل جمع اعداد یک تا N ، فرمول گاوس وجود دارد و نیاز به صرف زمان زیادی نیست.
جیمز لسترلینگ، ریاضیدان اسکاتلندی فرمول زیر را برای محاسبهی !N پیشنهاد کرده است :
در رابطه فوق عدد e ، یک عدد مشخص و مشهور در محاسبات لگاریتمی مانند عدد پی، در محاسبات دایره است. مقدار تقریبی عدد e برابر 2.7182 است. لازم به ذکر است که این عدد نیز مانند عدد پی یک عدد گنگ است و پایانی برای قسمت اعشاری آن وجود ندارد.
حالا به یک بحث جانبی بپردازیم، خطای نسبی!…………………………………………………………………………………………
فرض کنید که برای یک مسئله، یک مقدار دقیق و یک مقدار تقریبی بدست آید. اگر تفاوت این مقادیر دقیق و تقریبی برابر یک باشد، آیا محاسبات تقریبی دقت خوبی داشته است؟
هم بله و هم خیر! فرض کنید مقدار دقیق 0.01 باشد و مقدار تقریبی را 1.001 حساب کرده باشیم! یعنی جواب تقریبی حدوداً 100 برابر جواب دقیق است.
حالا فرض کنید که مقدار دقیق 1000 باشد و مقدار تقریبی 1001 بدست آمده است. در این صورت جواب تقریبی 1.001 برابر جواب دقیق است.
این یعنی نسبت خطای محاسبه به مقدار دقیق مهم است نه مقدار خود خطا! یعنی در اعداد بزرگ و کوچک مقدار خطاهای متفاوت قابل قبول میتواند باشد. مثلاً در 15 تن گندم
10 کیلوگرم کم و زیاد چندان مهم نیست ولی در خرید 200 گرم طلا، 10 گرم کم و زیاد شدن بسیار مهم است!
……………………………………………………………………………………………………………………………………
به ادامه بحث بپردازیم. فرمول محاسبهی خطای نسبی فرمول استرلینگ به صورت زیر است :
بیشترین مقدار ممکن این خطای نسبی برابر زیر است
یعنی هر چقدر عدد N بزرگتر باشد، مقدار خطای نسبی کوچکتر میشود.
مثال از کاربرد فرمول استرلینگ در محاسبه مقدار !15
مقدار دقیق برابر زیر است
1307674368000 = !15
مقدار فرمول استرلینگ
خطای نسبی این مقدار برابر 0.006 است! این یعنی یک تقریب بسیار خوب !
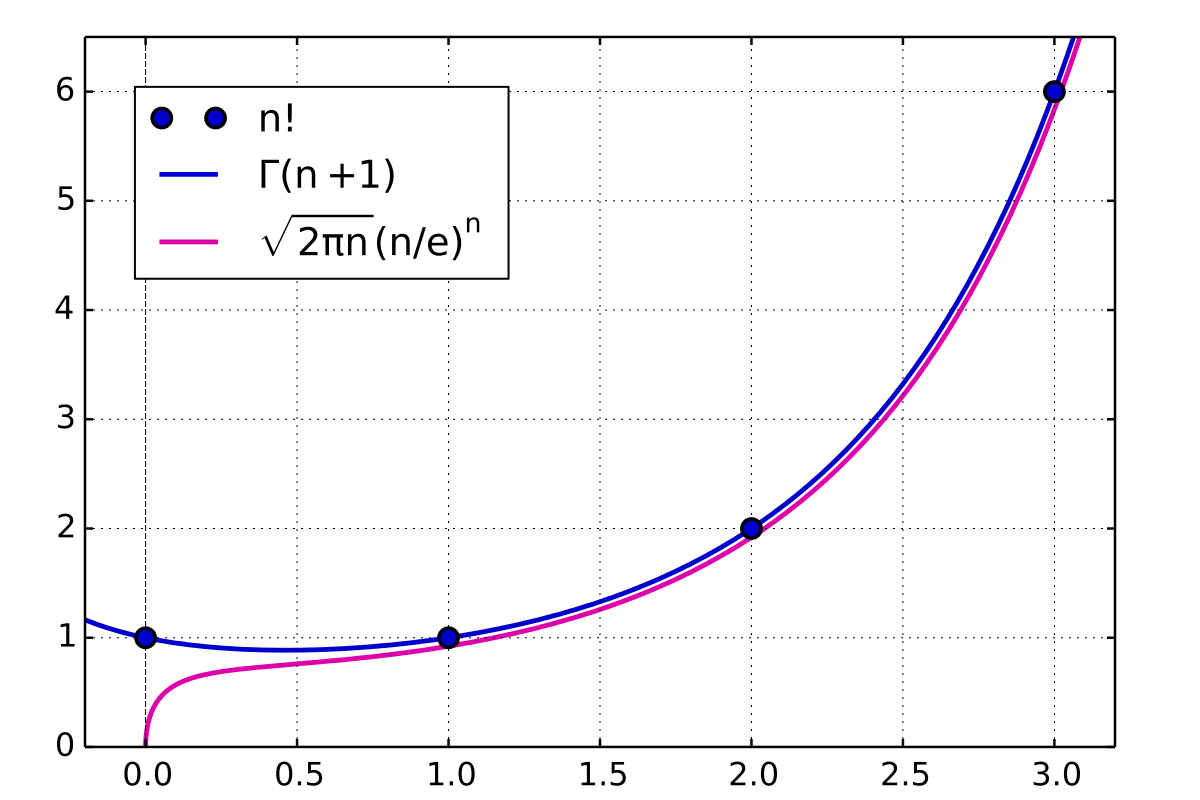
در نمودار تطبیق مقدارهای دقیق و تقریبی ناشی از فرمول استرلینگ را میتوان دید.

1 دیدگاه
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.






بخاطر وجود سایت کوشیار و کمک در زمینه سوالات ریاضی کمال تشکر دارم