حدس کولاتز در ریاضیات
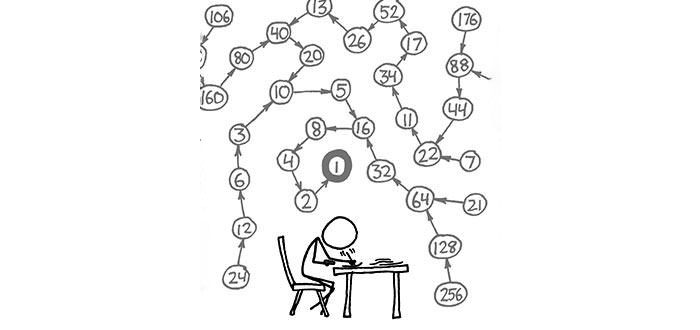
در این نوشته یک مسئلهی حل نشده در ریاضیات را بررسی میکنیم. حدس کولاتز !
این حدس، یک روند تکراری دارد. این روند با دستورهای سادهی زیر بیان میشود :
یک عدد طبیعی دلخواه در نظر بگیرید.
1 ) اگر این عدد زوج بود آن را تقسیم بر دو کنید.
2 ) اگر فرد بود ، سه برابر آن را بعلاوه یک کنید.
کولاتز بیان میکند با تکرار دو دستور سادهی بالا، روی اعداد بدست آمده ، زنجیره سرانجام حتماً به عدد ” یک ” میرسد.
مثلاً اگر با عدد 7 شروع کنیم. دنبالهی زیر بوجود میآید.
۷→۲۲→۱۱→۳۴→۱۷→۵۲→۲۶→۱۳→۴۰→۲۰→۱۰→۵→۱۶→۸→۴→۲→۱
مسئله فوق تا بحال اثبات نشده است! کولاتز در سال 1937 حدس فوق را مطرح کرد. این موضوع تا بحال اثبات نشده است
درستی حدس بالا به وسیلهی کامپیوترهای قدرتمند، تا عدد 2 به توان 60 نشان داده شده است. در عین حال چون اثبات منطقیای وجود ندارد، هنوز ممکن است عددی یافت شود که این حدس را نقض کند.

به عنوان یک نتیجهگیری میتوان گفت که اگر روند کولاتز رو معکوس کنیم. باید بتوان تمام اعداد طبیعی را ساخت. البته روند معکوس کولاتز به یک زنجیره خاص منحصر نیست و میتواند چند شاخه شود! مثل عدد 10 در شکل بالا ، که اگر معکوس روند کولاتز را دنبال کنیم به دو عدد 3 و 20 میرسیم.
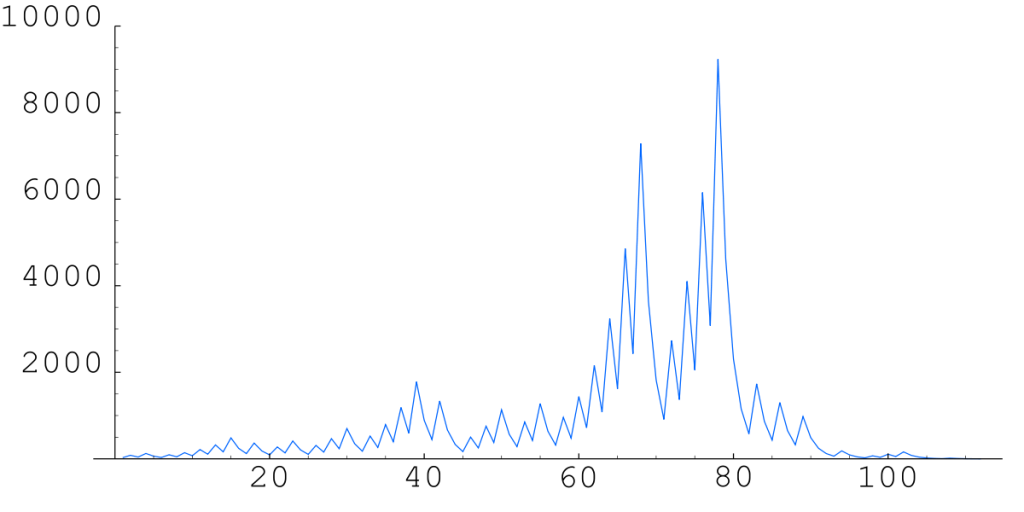
در حین بررسی دنباله کولاتز ممکن است به اعدادی به مراتب بزرگتر از عدد اولیه هم برسیم. ولی بعد از چند تکرار این اعداد دوباره کوچک میشوند تا به عدد یک برسیم. در شکل زیر روند تغییر اعداد دنبالهی کولاتز به ازای اینکه اولین عدد 27 باشد ، دیده میشود. محور افقی برابر تعداد تکرار و محور عمودی مقدار عدد دنباله را نشان میدهد. این سری عددی 111 عدد دارد و در بعضی مواقع مقدارش به 9000 نیز میرسد.
کوشیار جایی برای یادگیری!
ریاضی تکمیلی نهم
لینک دانلود پاسخ تشریحی سوالات صفحه 42 و 51 کتاب ریاضی تکمیلی نهم : لینک دانلود- به پایین صفحه بازشده بروید
لینک دانلود پاسخ تشریحی سوالات صفحه 51 بخش دوم کتاب ریاضی تکمیلی : page 51-2 math 9
لینک دانلود پاسخ تشریحی سوالات صفحه 52 کتاب ریاضی تکمیلی : page 52 math 9
لینک دانلود پاسخ تشریحی سوالات صفحه 52-53 کتاب ریاضی تکمیلی : page 52-53 math 9
10 دیدگاه
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.

سلام
من میتوانم حدس کولاتز را ثابت کنم. راهش پیدا کردم.
فقط نمیدونم چگونه به بهترین نحو ممکن مطرح کنم تا مطمعن باشم که به نام خودم ثبت خواهد شد.
سلام
چطوری حلش کردی. برای من در واتساپ پیام بده.
۰۹۱۴۳۱۸۲۹۸۴
من اثبات کردم اما نمیدونم به کی بگم ثبت کنه.و چجوری بایستی ثبت بشه.
اگر معلم ریاضی آشنایی میشناسید بهش اثباتتون رو نشدن بدید
اگر مورد تایید قرار گرفت
مدال فیلدز رو میبرید
البته باید دید اون معلم متوجه صحیح یا غلط بودن اثبات میشه یا نه
منم اثبات کردم
خیلی راحته
اینا مکانیسمش اینه
یا زوج باش و به دو تقسیمت کنم،یا زوجت میکنم و به دو تقسیمت میکنم
و واضحه که هر چقدر تقسیم کنیم نهایتا به یک میرسیم
تازه
شما میتونید به جای سه هر عدد فردی رو که دلتون بخواد بذارید و همین نتیجه رو ببینید
هیچ استثنایی هم نداره
سلام
ن به این سادگی هم نیست
چون اگر 3n+1 فقط یکبار به ۲ تقسیم بشه عدد بعدی افزایش پیدا می کته اگر مجده ۳برابر این عدد هم +یک فقط یکبار قابل تقسیم باشه بازهم شاهد افزایش جمله بعدی هستیم
مشگل اصلی اینه که معلوم نیست چند بار تقسیم بر دو میشه ابهام مسئله اینجاست
کاملا موافقم…دقیقا همینه…اصلا میشه ۳ برابرش نکرد .اگه زوج بود تقسیم بر ۲ اگه فرد بود بعلاوه یک یا منهای یک فرقی نداره
این سوال اثباتی نداره اصن فقط یه سوال فریب دهنده است.شاید به یک برسیم ولی اینو بدونید که طراح این سوال اینو میخواسته…………اطمینان دارم.
این سوال اثباتی نداره اصن فقط یه سوال فریب دهنده است.شاید به یک برسیم ولی اینو بدونید که طراح این سوال اینو میخواسته…………اطمینان دارم.